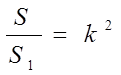Методика обучения содержанию темы

Содержание главы VII учебника «Геометрия 7-9» Л.С Атанасяна составляет материал, являющийся традиционным для любого курса планиметрии: пропорциональные отрезки, подобие треугольников, признаки подобия треугольников, отношение площадей подобных треугольников, подобие произвольных фигур. С помощью подобия треугольников доказывается одно из важных свойств треугольников: теорема о средней линии треугольника.

Усвоение учащимися признаков подобия треугольников и формирования умения применять их являются одной из основных задач этой главы. Это не случайно: свойства подобных треугольников будет многократно применяться в дальнейших главах курса, как планиметрии, так и стереометрии.

При изучении признаков подобия треугольников достаточно доказать два первых признака, так как первый признак доказывается с опорой на теорему об отношении площадей треугольников, имеющих равные углы, а доказательства двух других аналогичны и опираются на первый признак.

Рассмотрим методические рекомендации к изучению материала первой главы. Первый параграф главы «Определение подобных треугольников» начинается с введения понятия пропорциональных отрезков, данное понятие вводится на наглядном уровне. Для этого можно выполнить рисунок

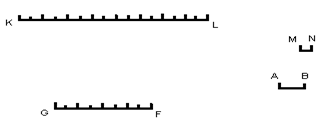
Рассмотрим отрезки KL и AB и отрезки GF и MN. Отрезок KL равен восьми отрезкам AB, а GF равен восьми отрезкам MN, т.е. выполняется равенство . Можно рассмотреть также отрезки KL и GF и отрезки AB и MN.Отрезок KL равен двум отрезкам MN , а AB равен двум отрезкам MN , т.е. выполняется равенство.

Значит отрезки KL и AB пропорциональны отрезкам GF и MN, а отрезки KL и GF пропорциональны отрезкам AB и MN.

При введении определения пропорциональные отрезки основное внимание учащихся необходимо направить на понимание того, что если в условии сказано: «…отрезок АВ делится точкой С в отношении 2:5…», то отрезок АВ разделен на семь частей, при этом отрезок АС содержит две части, а отрезок СВ содержит пять частей. Кроме того, они должны уметь записать в ходе решения задачи или в краткой записи условие отношение . Формирование умения применять понятие пропорциональности и навыка записи отношения разных величин является методической задачей не только геометрии, но и алгебры.

На закрепление этого навыка полезно выполнить следующие упражнения по готовому чертежу.

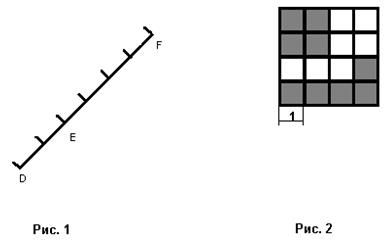
По данным рисунка 1 определите, как относятся отрезки:

а)DE к DF; б) EF к DF; в) DE к EF.

По данным рисунка 2 определите, как относится площадь заштрихованных квадратов к площади незаштрихованных квадратов.

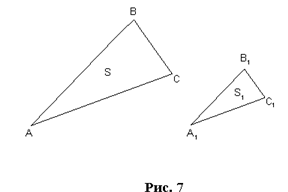
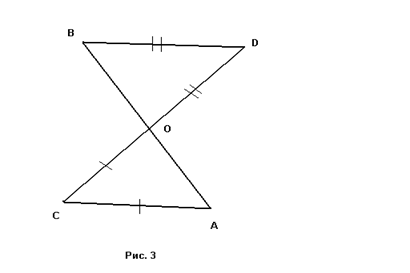
В учебнике перед введением определения подобных треугольников вводится понятие сходственных сторон. При его введении следует обратить внимание, что сходственные стороны лежат против равных углов и, наоборот против сходственных сторон лежат равные углы рис 3.

Поэтому, если в условии сказано: « Треугольники ABC и DEF подобны и у них <A=<D, <B=<E, <C=<F…», то учащиеся должны уметь записать пропорциональность сходственных сторон: . А если в условии сказано: «Треугольники ABC и DEF подобны и у них …» , то учащиеся должны уметь записать равенство углов : <A=<D, <B=<E, <C=<F.

Для формирования умения записывать пропорциональность сходственных сторон и равенство соответствующих углов в подобных треугольниках можно предложить учащимся следующие упражнения.

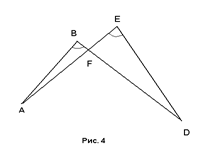
Треугольники, данные на рисунках 3 и 4 подобны. Запишите отношение сходственных сторон и равенство соответствующих углов.

Радиусы окружностей, изображенных на рисунке 5 относятся как 2:1. Запишите отношение сходственных сторон и равенство соответствующих углов.

Опираясь на определение подобных треугольников, докажите, что равносторонние треугольники подобны (Рис. 5).

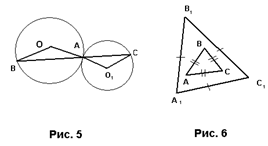
После формулировки теоремы об отношении подобных треугольников и выполнения рисунка 6 следует сделать краткую запись условия и заключения теоремы.

Похожие статьи:

Этапы становления воспитательной системы школы
Условно можно выделить четыре этапа в развитии воспитательной системы. Первый этап развития воспитательной системы - этап становления. Одной из основных целей воспитательной системы на первом этапе является создание воспитательного коллектива школы. Предпосылками для объединения детей и взрослых в ...

Состояние проблемы формирования знаний о русских исследователях-путешественниках в школьных учебниках, программах и контрольно-измерительных материалах по географии
Как известно, деятельность учителя при реализации тех или иных идей, определенных учебными программами, ориентируется в первую очередь на школьные учебники. Поэтому, чтобы установить, имеется ли реальная возможность для реализации идеи формирования географической культуры личности на основе знаний ...

Физико-математическая школа Томского государственного университета
Цель создания ТФМШ – отбор и воспитание талантливой учащейся молодежи путем обучения и привлечения их к участию в научной деятельности. Основными направлениями работы школы являлись и остаются на настоящем этапе развития школы: - профильное углубленное обучение школьников 8-11-х классов; - научно-и ...