Математическая карта темы «Подобные треугольники»

Понятий в теме 6. Они даются в конструктивном виде. Для их усвоения требуются такие опорные знания как длина отрезка, отношение отрезков, элементы, как произвольного, так и прямоугольного треугольника и их буквенное обозначение.

Подведение под понятие осуществляется с помощью учителя, опираясь на предыдущие знания. В основном ошибки могут быть вызваны при составлении отношений сходственных сторон из-за неумения учеников определять соответственные сходственные стороны.

Для качественного усвоения знаний, учителю необходимо добиться от учеников понимания материала и применение их в практике. Для этого следует проводить работу по карточкам и готовым чертежам. Также проводить устные опросы учащихся.

Анализ утверждений

Утверждений в теме 9. Каждое утверждение представлено с доказательством. Утверждения следуют в определенной логике, доказательство последующего опираются на ранее доказанные утверждения. Для качественного усвоения знаний учениками необходимо проводить устные опросы и самостоятельные работы. Важные, часто используемые свойства можно оформить на карточках каждому из учеников. Например, признаки равенства треугольников.

Анализ алгоритмов и правил

Алгоритм определения подобия треугольников.

1. Определите соответствующие известные элементы треугольников.

2. Определите количество известных соответственно равных углов треугольников.

<A=<A1, <B=<B1,

следовательно треугольники подобны по 1 признаку.

<A=<A1.

AB/A1B1=AC/ A1C1 =к,

треугольники подобны по 2 признаку.

AB/ A1B1 AC/ A1C1,

треугольники не подобны.

Не известно равенство соответствующих углов.

AB/ A1B1=AC/ A1C1 =BC/ B1C1,

треугольники подобны по 3 признаку.

AB/ A1B1AC/ A1C1 BC/B1C1 ,

треугольники не подобны.

Пример решения задачи с использованием данного алгоритма:

Для определения высоты столба A1C1 использован шест, чему равна высота столба, если BC1=6,3; BC=3,4; AC=1,7

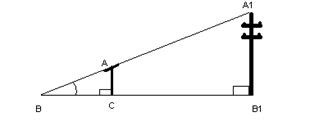
Из рисунка видно, что нам даны два прямоугольных треугольника у которых известно:

1. BC1, BC, AC.

2. <BCA=<BC1A1 прямые углы; <ABC=<A1BC1 как общие углы.

Следовательно, треугольники подобны по первому признаку.

Из определения подобных треугольников следует:

AB/A1B=AC/ A1C1=BC/BC1, т.е A1C1= (BC1/BC)*AC

A1C1=3,15.

Данный алгоритм обладает следующими свойствами:

Позволяет установить, подобны ли данные треугольники. Его можно применять для любой задачи в которой необходимым шагом решения является определение подобия треугольников. Каждый шаг алгоритма четко определен и последователен.

Анализ задачного материала

Задачный материал учебника геометрии Л.С. Атанасяна не разбивается по уровням сложности, представлен отдельным блоком в конце каждого пункта. В конце главы 12 представлены вопросы для повторения и дополнительные задачи по всей главе.

Все задачи главы можно разбить на следующие группы:

1. На отношение сторон, пропорциональность отрезков и использование определения подобных треугольников(11 номеров).

Пример:

Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Подобны ли треугольники ABC и DEF, если <A=1060, <B=340, <E=1060, <F=400, AC=4,4 , BC=7,6 , AB=5,2 , DE=15,6 , DF= 22,8 , EF= 13,2 .

2. На отношение площадей подобных треугольников(6 номеров).

Пример:

Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второго треугольника равна 9 м. Найдите сходственную сторону первого треугольника.

Похожие статьи:

Виды игр, используемые на занятиях, методика их проведения
Игровые упражнения уже в самом начале урока настраивают ребят на дальнейшую активную речевую деятельность. Но, чтобы этот интерес не угас, на каждом кружковом занятии я стараюсь использовать что-то новое или уже хорошо забыто старое, а также применять игры наиболее полюбившиеся детям. Существует бо ...

Творческие способности и эмоционально–коммуникативные качества учителя-филогога
Современная педагогическая наука делает акцент на правомерности и эффективности роли учителя – соучастника «образовательных событий», в которых осуществляется концентрация личного эстетического и культурного опыта учеников. В этом контексте формируется сложная в педагогическом отношении задача, сто ...

Место художественной литературы на уроке истории и принципы ее отбора
Основные знания по истории учащиеся получают через рассказ учителя. Нити рассказа прокладывают в сознании детей связи с прошлым народа и страны. Слово учителя, предельно точное, полное стремительной мысли и неподдельного чувства, во многом предопределяет успех обучения. Однако учитель не всегда нах ...