Решение матричной игры в смешанных стратегиях

Если платежная матрица не имеет седловой точки, т.е. a <b и , то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами.

Определение 1. Сложная стратегия, состоящая в случайном применении всех стратегий с определенными частотами, называется смешанной.

В игре, матрица которой имеет размерность m ´ n, стратегии первого игрока задаются наборами вероятностей (x1, x2, ., xm), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассмотреть как m-мерные векторы, для координат которых выполняются условия

, xi ³ 0, .

Аналогично для второго игрока наборы вероятностей определяют n-мерные векторы (y1, y2, ., yn), для координат которых выполняются условия

= 1, yj ³ 0, .

Выигрыш первого игрока при использовании смешанных стратегий определяют как математическое ожидание выигрыша, т.е. он равен

.

Теорема 1. (Неймана. Основная теорема теории игр) Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий. Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: a £ v £ b. Применение первым игроком оптимальной стратегии опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение

, .

Аналогично для второго игрока оптимальная стратегия опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение

, .

Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и не доминирующих стратегий.

Определение 2. Дублирующими называются стратегии, у которых соответствующие элементы платежной матрицы одинаковы.

Определение 3. Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то i-я стратегия игрока А называется доминирующей над k-й стратегией. Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я стратегия игрока В называется доминирующей над k-й стратегией.

Пример. Рассмотрим игру, представленную платежной матрицей

.

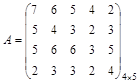Похожие статьи:

Формирование эстетических принципов в театре Вахтангова
Режиссерская манера Вахтангова претерпела значительную эволюцию за 10 лет его активной творческой деятельности. От предельного психологического натурализма первых постановок он пришел к романтической символике «Росмерсхольма». А далее — к преодолению «интимно-психологического театра», к экспрессион ...

Сущность воспитательной системы школы
Воспитательная система школы – это совокупность взаимосвязанных компонентов (воспитательные цели, люди, их реализующие, их деятельность и общение, отношения, жизненное пространство), составляющая целостную социально-педагогическую структуру школы и выступающая мощным и постоянно действующим факторо ...

Учебно-воспитательное значение экскурсий
Преподавание химии в школе нельзя ограничивать только сведениями из учебников и тем материалом, который учащиеся получают на уроках. Большую роль учителю могут оказать учебные экскурсии на различные предприятия и народнохозяйственные объекты. Экскурсии имеют не только познавательное значение, но ещ ...