Методика обучения учащихся решению задач
Этапы решения геометрических задач:
I Этап: Выделение требования задачи, объектов и отношений между ними, выполнение рисунка, отметка на нем данных и искомых элементов, краткая запись условия и заключения задачи.
Какая фигура дана?
Что известно?
Что необходимо найти?
II Этап: Анализ условия и требования задачи (поиск метода решения).
Под анализом условия задачи будем понимать выявление такой информации, которая непосредственно не задана условием, но присуща ему.
III Этап: Осуществление плана решения (оформление решения).
Две формы оформления решения задачи:
в начале записываем полученный вывод и здесь же в строчку записываем аргументы, на основании которых он был сделан
заполнение таблицы.
IV Этап: Изучение найденного решения.
Исследование задачной ситуации можно осуществить со стороны:
способа поиска решения задачи
способа развития ученика
способа систематизации знаний
Рассмотрим методику решения задачи на примере решения задачи 543.
Докажите, что отношение сходственных сторон подобных треугольников равно отношению высот, проведенным к этим сторонам.
|
Деятельность учителя. |
Деятельность учеников. |
|
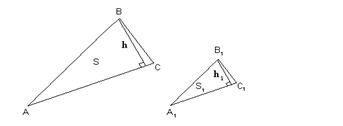
I Этап: Давайте изобразим рисунок и запишем краткое условие задачи.
Внимательно прочитайте условие задачи и определите, что нам дано. Что нужно найти или доказать? Возьмем стороны AC и A1C1 за соответствующие сходственные стороны, тогда краткое условие: Дано: DABC~DA1B1C1 , h- высота DABC, h1-высота DA1B1C1 Доказать: II Этап: Давайте обозначим площади соответствующих треугольников за S и S1 соответственно. Посмотрите на заключение задачи (то, что нужно доказать). Чему равно отношение сходственных сторон подобных треугольников? Посмотрите на рисунок, нам дана высота. Можем ли мы выразить площадь треугольника? Чему равна площадь треугольника ABC? А площадь треугольника A1B1C1? Что получим, если составим отношение площадей? Но треугольники у нас подобные. Чему равно отношение площадей подобных треугольников? Но Приравняв два равенства |
Нам даны два подобных треугольника и высоты проведенные к соответствующим сходственным сторонам. Докажите, что отношение сходственных сторон подобных треугольников равно отношению высот, проведенным к этим сторонам. (Дети в тетрадях делают рисунок и записывают краткое условие)
Да.
Да, можем. |
III этап:
Оформление доказательства задачи в тетради у учеников должно быть следующим.
Доказательство:
1) S-площадь DABC, S1-площадь DA1B1C1
2) ![]() , т.к. DABC~DA1B1C1
, т.к. DABC~DA1B1C1
3) ![]() , по определению.
, по определению.
4) 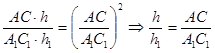 , задача решена.
, задача решена.
Поставленные в реферате цели и задачи были реализованы. Тема «Подобие треугольников» в различных учебниках рассматривается в разной последовательности. Одни и те же понятия в различных учебных пособиях и учебниках определяются по-разному, а также различно акцентирования внимания на содержание данной темы. Разработано приложение в которое входит два конспекта уроков, практикум по решению задач и примерные задания контрольной работы на заключительном этапе изучения темы.
Похожие статьи:
Некоторые показатели готовности к обучению детей с особыми проблемами
развития
Формирование готовности к школьному обучению у ребенка в значительной степени связано с развитием его нервно-психических функций, что, в свою очередь, обусловлено созреванием организма и, прежде всего, ЦНС. Вместе с тем созревание тех или иных функций ускоряется в процессе активного функционировани ...
Методики и игры по развитию произвольного внимания учащихся начальной школы
На основе данных диагностики внимания учитель может провести групповую или индивидуальную работу с учащимися по развитию произвольного внимания. Для этого существует огромное количество методик, игр и упражнений. Некоторые из них мы рассмотрим. Методики по развитию общей внимательности, наблюдатель ...
Место компьютера в начальной школе
Почему маленьким детям на уроке не всегда интересно? То устанут, то скука одолеет. Почему жизнь школы порой непохожа на цветной, яркий мир, который сопровождает ребенка в его общении с друзьями и книгами? Школа и школьная жизнь должна увлекать ребенка, вводя его в удивительный мир познания. Вот тут ...

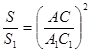
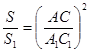 и
и