Игры с природой

В рассмотренных выше матричных играх предполагалось, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.

Условия игры задаются матрицей

.

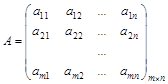Пусть игрок А имеет стратегии А1, А2, …, Аm, а природа - состояния В1, В2, …, Вn. Наиболее простой является ситуация, когда известна вероятность pj каждого состояния природы Вj. При этом, если учтены все возможные состояния, p1 + p2 + … + pj + … + pn = 1.

Если игрок А выбирает чистую стратегию Аi, то математическое ожидание выигрыша составит p1 ai1 + p2 ai2 + … + pn ain. Наиболее выгодной будет та стратегия, при которой достигается

(p1 ai1 + p2 ai2 + … + pn ain).

Если информация о состояниях с природой мала, то можно применить принцип недостаточного основания Лапласа, согласно которому можно считать, что все состояния природы равновероятностны:

,

т.е. стратегию, для которой среднее арифметическое элементов соответствующей строки максимальное.

Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.

1. Критерий Вальда. Рекомендуется применять максиминную стратегию. Она выбирается из условия

и совпадает с нижней ценой игры. Критерий является пессимистическим, считается, что природа будет действовать наихудшим для человека способом.

2. Критерий максимума. Он выбирается из условия

.

Критерий является оптимистическим, считается, что природа будет наиболее благоприятна для человека.

3. Критерий Гурвица. Критерий рекомендует стратегию, определяемую по формуле

,

где a - степень оптимизма и изменяется в диапазоне .

Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего поведения природы. При a = 1 критерий превращается в критерий Вальда, при a = 0 - в критерий максимума. На a оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем больше последствия ошибочных решений, больше желания застраховаться, тем a ближе к единице.

4. Критерий Сэвиджа. Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.

.

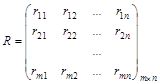Похожие статьи:

Анализ программы кружка «МастерОк»
В ХХI веке технологическое образование становится объективной необходимостью. Настоящий этап развития общества отличается интенсивным внедрением во все сферы человеческой деятельности новых, наукоёмких и высоких технологий, обеспечивающих более полную реализацию потенциальных творческих способносте ...

Игры на формирование межличностных отношений
«Найди друга» (для детей 5 лет) Упражнение выполняется среди детей или же между родителями и их детьми. Одной половине завязываются глаза, предлагают походить по помещению, где нужно найти и узнать друга (или своего родителя). Узнать можно с помощью рук, используя прикосновения, ощупывание волос, о ...

Учебно-воспитательное значение экскурсий
Преподавание химии в школе нельзя ограничивать только сведениями из учебников и тем материалом, который учащиеся получают на уроках. Большую роль учителю могут оказать учебные экскурсии на различные предприятия и народнохозяйственные объекты. Экскурсии имеют не только познавательное значение, но ещ ...