Решение матричной игры в чистых стратегиях

Рассмотрим простейшую математическую модель конечной конфликтной ситуации, в которой имеется два участника и выигрыш одного равен проигрышу другого. Такая модель называется антагонистической игрой двух лиц с нулевой суммой. Игра состоит из двух ходов: игрок А выбирает одну из возможных стратегий Аi, , а игрок В выбирает одну из возможных стратегий Вj, . Каждый выбор производится при полном незнании выбора соперника. В результате выигрыш игроков составит соответственно aij и - aij. Цель игрока А - максимизировать величину aij, а игрока В - минимизировать эту величину.

Определение 1. Матрица, составленная из величин aij, ,,

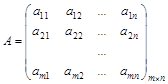
называется платежной матрицей, или матрицей игры. Каждый элемент платежной матрицы aij, ,равен выигрышу А (проигрышу В), если он выбрал стратегию Аi, , а игрок В выбирал стратегию Вj, .

Пример. В игре участвуют первый и второй игроки, каждый из них может записать независимо от другого цифры 1, 2 и 3. Если разность между цифрами, записанная игроками, положительна, то первый игрок выигрывает количество очков, равное разности между цифрами, и, наоборот, если разность отрицательна, то выигрывает второй игрок. Если разность равна нулю, то игра заканчивается вничью.

У первого игрока три стратегии (варианта действия): А1 (записать 1), А2 (записать 2), А3 (записать 3); у второго игрока также три стратегии: В1, В2, В3 (табл.1).

Таблица 1

Задача первого игрока - максимизировать свой выигрыш. Задача второго игрока - минимизировать свой проигрыш или минимизировать выигрыш первого игрока. Платежная матрица имеет вид

.

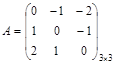Задача каждого из игроков - найти наилучшую стратегию игры, при этом предполагается, что противники одинаково разумны и каждый из них делает все, чтобы получить наибольший доход.

Найдем наилучшую стратегию первого игрока. Если игрок А выбрал стратегию Аi, , то в худшем случае (например, если его ход известен В) он получит выигрыш . Предвидя такую возможность, игрок А должен выбрать такую стратегию, чтобы максимизировать свой минимальный выигрыш.

.

Определение 2. Величина a - гарантированный выигрыш игрока А называется нижней ценой игры. Стратегия Aiопт, обеспечивающая получение выигрыша a, называется максиминной.

Если первый игрок будет придерживаться своей максиминной стратегии, то у него есть гарантия, что он в любом случае выиграет не меньше a.

Похожие статьи:

Мотивы досуга
Культурно-досуговая деятельность ребёнка связана с удовлетворением познавательных и практических потребностей, которые основываются на мотиве деятельности. Освоение реального мира в процессе культурно-досуговой деятельности требует от ребёнка активности, напряжения, способности к саморазвитию и сам ...

Методические рекомендации по проведению недели географии «Памяти знаменитого полярника – Г.Я. Седова»
Неделя географии в школе является комплексным мероприятием, сочетающим в себе разнообразные формы внеурочной работы: вечера, конференции, смотры-конкурсы географических знаний, конкурсы газет, рефератов и т.д. Поэтому подготовка и проведение предметных недель требуют больших временных, ресурсных и ...

Коммуникативный аспект изучения предложения
Наиболее существенным свойством предложения для представителей коммуникативного синтаксиса является способность предложения выступать в качестве средства общения (коммуникации). Коммуникативный аспект предложения проявляется в так называемом актуальном членении, при наличии которого в предложении в ...