Сведение матричной игры к задаче линейного программирования

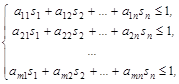(4) где , . (5)

По условию y1 + y2 + … +yn = 1. Разделим обе части этого равенства на v.

.

Оптимальная стратегия (y1, y2, ., yn) игрока В должна минимизировать величину v, следовательно, функция

(6)

должна принимать максимальное значение.

Получена задача линейного программирования: найти максимум целевой функции (6) при ограничениях (4), причем на переменные наложено условие неотрицательности (5).

Таким образом, для нахождения решения игры имеем симметричную пару двойственных задач линейного программирования. Можно найти решение одной из них, а решение второй находится с использованием теории двойственности.

Пример. Найти решение игры, заданной матрицей

.

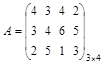a = max (2, 3,1) = 3, b = min (4, 5, 6,5) = 4, a ¹ b, .

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.

Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования:

,

, .

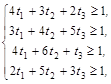
Для нахождения оптимальной стратегии игрока В имеем следующую задачу линейного программирования:

,

, .

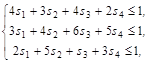
Оптимальные решения пары двойственных задач имеют вид

, , .

Учитывая соотношения между xi и ti, yj и sj, а также равенство

,

можно найти оптимальные стратегии игроков и цену игры:

(1/2, 1/2, 0), (3/4, 0, 0, 1/4), v=7/2.

Похожие статьи:

Психологические особенности способностей
Способности – это такие психологические способности человека, от которых зависит успешность приобретения знаний, умений, навыков, но которые сами к наличию этих знаний и умений не сводятся. По оценке на экзамене, ответу у доски, удачно или неудачно выполненной контрольной работе невозможно сделать ...

Цель обучения пунктуации. Место пунктуации в школьном курсе русского языка
Конечная цель обучения детей пунктуации в школе: сформировать у них пунктуационную грамотность, под которой понимается умение пишущего правильно употреблять знаки препинания членения предложений и текста на смысловые отрезки, а читающего - адекватно с пишущим понимать написанное. Существуют два уро ...

Классификация праздников для детей младшего школьного возраста
Физкультурные праздники в начальных классах обычно посвящаются каким-либо знаменательным датам. В программу таких праздников, как правило, включают парад участников и торжественное открытие праздника с подъемом флага, массовые гимнастические выступления, простейшие спортивные соревнования, игры, ат ...