Решение игр графическим методом

если второй игрок с вероятностью 2/3 будет применять первую стратегию и с вероятностью 1/3 вторую, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более 5/3.

Второй случай. Рассмотрим игру (2 ´ n) с матрицей

.

Для каждой из n стратегий игрока В строится соответствующий ей отрезок на плоскости. Находится нижняя граница выигрыша, получаемого игроком А, и определяется точка на нижней границе, соответствующая наибольшему выигрышу. Выделяются две активные стратегии игрока В, отрезки которых проходят через данную точку. Далее рассматриваются только эти две стратегии игрока В. Игра сводится к игре с матрицей (2 ´ 2). Оптимальные стратегии и цену игры находят по формулам (1) - (3).

Пример 2. Найти решение игры, заданной матрицей

.

a = max (1,1) = 1, b = min (4, 3, 3,4) = 3, a ¹ b, .

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям второго игрока. (см. рис.4)

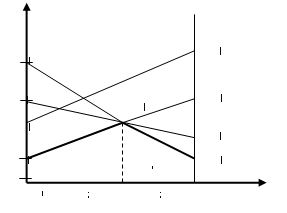Нижней границей выигрыша для игрока А является ломаная В3КВ4. Стратегии В3 и В4 являются активными стратегиями игрока В. Точка их пересечения К определяет оптимальные стратегии игроков и цену игры. Второму игроку невыгодно применять стратегии В1 и В2, поэтому вероятность их применения равна нулю, т.е. у1 = у2= 0. Решение игры сводится к решению игры с матрицей (2 ´ 2)

.

a = max (1,1) = 1, b = min (3,4) = 3, a ¹ b, .

По формулам (1) - (3) находим оптимальные стратегии и цену игры:

x1 = 2/5, x2 = 3/5; y3 = 3/5, y2 = 2/5; v =11/5.

Ответ. Оптимальные смешанные стратегии игроков (2/5, 3/5) и (0, 0, 3/5, 2/5), цена игры составляет v =11/5.

Данный ответ означает следующее:

если первый игрок с вероятностью 2/5 будет применять первую стратегию и с вероятностью 3/5 вторую, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее 11/5;

если второй игрок с вероятностью 3/5 будет применять третью стратегию, с вероятностью 2/5 четвертую и не будет использовать первую и вторую стратегии, то при достаточно большом количестве игр с данной матрицей его проигрыш в среднем составит не более 11/5.

Третий случай. Рассмотрим игру (m ´ 2) с матрицей

.

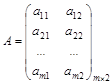Решение игры может быть получено аналогично случаю два. Для каждой из m стратегий игрока А строится соответствующий ей отрезок на плоскости.

Находится верхняя граница проигрыша, получаемого игроком В, и определяется точка на нижней границе, соответствующая наименьшему проигрышу. Выделяются две активные стратегии игрока А, отрезки которых проходят через данную точку.

Далее рассматриваются только эти две стратегии игрока А. Игра сводится к игре с матрицей (2 ´ 2). Оптимальные стратегии и цену игры находят по формулам (1) - (3).

Пример 3. Найти решение игры, заданной матрицей

.

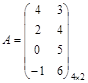a = max (3, 2, 0, - 1) = 3, b = min (4,6) = 4, a ¹ b, . Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий. Построим на плоскости отрезки, соответствующие стратегиям первого игрока. (см. рис.5).

Верхней границей проигрыша для игрока В является ломаная А1КА4. Стратегии А1 и А4 являются активными стратегиями игрока А. Точка их пересечения К определяет оптимальные стратегии игроков и цену игры. Первому игроку невыгодно применять стратегии А2 и А3, поэтому вероятность их применения равна нулю, т.е. x2 = x3= 0. Решение игры сводится к решению игры с матрицей (2 ´ 2)

Похожие статьи:

Анализ деятельности социального педагога МОУ СОШ № 103 по первичной профилактике наркотической зависимости у старших подростков
Средняя общеобразовательная школа № 103 расположена на окраине микрорайона Уралмаш, в непосредственной близости от всемирно известного завода "Уралмаш" (УЗТМ). Являясь важным стратегическим объектом государственного значения, огромным промышленным центром с богатой историей и субкультурой ...

Формирование произносительных навыков при работе с поэтическим материалом на уроке английского языка
Работа над произносительной стороной речи ведется на всех ступенях обучения языку. При этом учащиеся с большим желанием и старанием работают над отдельными звуками, труднопроизносимыми словами и интонацией, если они представлены в рифмованной форме. Для решения вопросов, связанных с обучением произ ...

Понятие просодической стороны речи
Овладение родным языком, развитие речи является одним из самых важных приобретений ребенка в дошкольном детстве и рассматривается в современном дошкольном воспитании как общая основа воспитания и обучения детей. В детском саду дошкольники, усваивая родной язык, овладевают важнейшей формой речевого ...