Классификация методов обучения в дидактике

е) самостоятельное выполнение произвольных заданий.

Методы научного познания в обучении математике.

К ним относятся:

1) логические методы познания: индукция, дедукция, анализ, синтез, сравнение, аналогия, обобщение, конкретизация, моделирование, классификация, доказательство.;

2) эмпирические методы познания.

Наблюдение, описание, измерение и эксперимент, которые не являются характерными для математики. История развития математики свидетельствует о том, что эмпирические методы сыграли неоценимую роль в зарождении математических знаний, становлении математики как науки, самостоятельной теоретической дисциплины. Школьное обучение математике в определенной мере повторяет ее исторический путь развития. Использование средств наглядности и ТСО предполагает применение различных эмпирических методов, помогающих избежать пассивной созерцательности, активизировать действия учащихся, вовлечь их в целенаправленную работу.

Задача. Найти все такие натуральные числа, квадрат которых оканчивается цифрой 7.

Поиск решения данной задачи предполагает небольшой числовой эксперимент и формулирование гипотезы в процессе обобщения полученных данных.

Метод измерения применим к поиску решения планиметрических задач, когда производим инструментальное исследование чертежа данной фигуры. Измерение: вывод о сумме внутренних углов в произвольном треугольнике, для чего учащимся предлагается вырезать из бумаги остроугольный, тупоугольный треугольники, транспортиром измерить величины их углов и найти их сумму: . Опыт: по табличным данным или отмеченным точкам на координатной плоскости определить вид функции:

а) ; б) ; в) ; г) .

Наблюдение: простые и составные числа; сформулировать определения. Простое ли число 1?

3) математические методы познания:

а) метод математических моделей. Математическая модель – описание какого-либо класса явлений реального мира на языке математики. Метод моделирования дает возможность применять математический аппарат к решению практических задач. Понятие числа, геометрической фигуры, уравнения, неравенства, функции, производной являются примерами математических моделей.

К методу математического моделирования в учебном процессе приходится прибегать при решении любой задачи с практическим содержанием. Чтобы решить такую задачу математическими средствами, ее необходимо вначале перевести на язык математики (построить модель), используя абстракции отождествления, идеализации, обобщения.

Задача. 6 коров за 3 дня съедают траву на участке 0,2 га, 8 коров за 4 дня съедают траву на участке 0,3 га. Сколько дней смогут пастись 12 коров на участке площадью 0,6 га? (Прирост травы на участке пропорционален его площади и времени).

x – количество травы, съедаемое одной коровой в день;

y – начальное количество травы на 1 га;

z – прирост травы на 1 га в день;

6 коров за 3 дня съедают траву на участке 0,2 га:

6*х*3=у*0,2+3*z*0,3.

8 коров за 4 дня съедают траву на участке 0,3 га:

8*х*4=у*0,3+4*z*0,3

Решим эту систему:

Определим первоначальное количество травы на одном га:

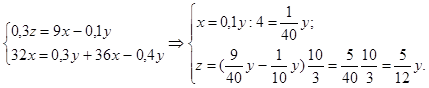
12 коров за t дней съедают траву на участке 0,6 га:

Похожие статьи:

Что такое лечебная педагогика
Лечебная педагогика – это система лечебно-педагогических мероприятий, имеющих целью предупреждение, лечение и коррекцию различных отклонений в развитии, нервно-психических и соматических нарушений, которые могут привести к стойкой инвалидизации, школьной и социальной дезадаптации. Лечебная педагоги ...

Формирование пунктуационной зоркости
Пунктуационная зоркость - это, во-первых, умение видеть в готовом предложении смысловой отрезок, требующий выделения знаками препинания, во-вторых, предвидеть те или иные смысловые отрезки, необходимые для выражения определенного дополнительного значения. Не владея пунктуационной зоркостью, ученик ...

Описание методики исследования, направленного на выявление предпосылок дисграфии у детей с ОНР III уровня старшего дошкольного возраста
В проведении констатирующего эксперимента по выявлению предпосылок дисграфии у детей старшего дошкольного возраста я воспользовалась опытом работы психолого-педагогического центра «Здоровье» Петроградского района Санкт-Петербурга. Это исследование было ориентировано непосредственно на выявление пре ...