Решение матричной игры в смешанных стратегиях

Если платежная матрица не имеет седловой точки, т.е. a <b и , то поиск решения игры приводит к применению сложной стратегии, состоящей в случайном применении двух и более стратегий с определенными частотами.

Определение 1. Сложная стратегия, состоящая в случайном применении всех стратегий с определенными частотами, называется смешанной.

В игре, матрица которой имеет размерность m ´ n, стратегии первого игрока задаются наборами вероятностей (x1, x2, ., xm), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассмотреть как m-мерные векторы, для координат которых выполняются условия

, xi ³ 0, .

Аналогично для второго игрока наборы вероятностей определяют n-мерные векторы (y1, y2, ., yn), для координат которых выполняются условия

= 1, yj ³ 0, .

Выигрыш первого игрока при использовании смешанных стратегий определяют как математическое ожидание выигрыша, т.е. он равен

.

Теорема 1. (Неймана. Основная теорема теории игр) Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий. Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: a £ v £ b. Применение первым игроком оптимальной стратегии опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение

, .

Аналогично для второго игрока оптимальная стратегия опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение

, .

Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и не доминирующих стратегий.

Определение 2. Дублирующими называются стратегии, у которых соответствующие элементы платежной матрицы одинаковы.

Определение 3. Если все элементы i-й строки платежной матрицы больше соответствующих элементов k-й строки, то i-я стратегия игрока А называется доминирующей над k-й стратегией. Если все элементы j-го столбца платежной матрицы меньше соответствующих элементов k-го столбца, то j-я стратегия игрока В называется доминирующей над k-й стратегией.

Пример. Рассмотрим игру, представленную платежной матрицей

.

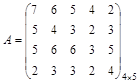Похожие статьи:

Профильные школы с физико-математическим уклоном в Западно-Сибирском регионе
В практике обучения интеллектуально одаренных детей более перспективным направлением считается создание классов (школ), ориентированных на специализированную предметную подготовку учащихся. Основная педагогическая задача смещается с развития общих способностей школьников к поиску способа реализации ...

Методы и формы экологического образования
Б.Т. Лихачев методы и формы экологического образования и воспитания условно разделяет на несколько групп. Это: школьные и внешкольные методы формирования сознания и развития мышления, научение умениям и навыкам практически направленной деятельности, развитие нравственно-правовой ответственности, эс ...

Логико-математический анализ темы: «Подобие треугольников»
В школьном курсе геометрии тема 'Подобие треугольников' рассматриваются в 8 классе. В учебнике по “Геометрии 7-9 класс” Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина данная тема рассматривается после темы “Площади”. Возьмем этот учебник за основной и проанализируем его: 1. Структ ...