Сведение матричной игры к задаче линейного программирования

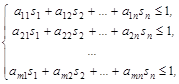(4) где , . (5)

По условию y1 + y2 + … +yn = 1. Разделим обе части этого равенства на v.

.

Оптимальная стратегия (y1, y2, ., yn) игрока В должна минимизировать величину v, следовательно, функция

(6)

должна принимать максимальное значение.

Получена задача линейного программирования: найти максимум целевой функции (6) при ограничениях (4), причем на переменные наложено условие неотрицательности (5).

Таким образом, для нахождения решения игры имеем симметричную пару двойственных задач линейного программирования. Можно найти решение одной из них, а решение второй находится с использованием теории двойственности.

Пример. Найти решение игры, заданной матрицей

.

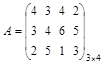a = max (2, 3,1) = 3, b = min (4, 5, 6,5) = 4, a ¹ b, .

Игра не имеет седловой точки. Оптимальное решение следует искать в области смешанных стратегий.

Для определения оптимальной стратегии игрока А имеем следующую задачу линейного программирования:

,

, .

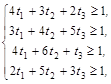
Для нахождения оптимальной стратегии игрока В имеем следующую задачу линейного программирования:

,

, .

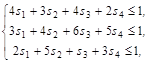
Оптимальные решения пары двойственных задач имеют вид

, , .

Учитывая соотношения между xi и ti, yj и sj, а также равенство

,

можно найти оптимальные стратегии игроков и цену игры:

(1/2, 1/2, 0), (3/4, 0, 0, 1/4), v=7/2.

Похожие статьи:

Соединение части вида и части разреза
Рис.13.Соединение части вида части разреза Форма многих деталей такова, что при их изображении недостаточно дать только вид или только разрез, так как по разрезу иногда нельзя представить внешнюю форму детали. При изображении подобных деталей необходимо дать как вид, так и разрез, т. е. выполнить д ...

Психолого-педагогическое обоснование
Понятие «компетентность» означает способность человека эффективно взаимодействовать со своим окружением. Социальная компетентность связана с социальным взаимодействием и может быть отождествлена, поскольку речь идет о способности человека, с социальной квалификацией и социальной подготовленностью. ...

Специфика правил при обучении письму леворуких детей
Обучая и развивая леворукого ребенка следует помнить, что речь дошкольников подчиняется закономерностям не логического, а непосредственно чувственного восприятия, которое обеспечивается деятельностью правого полушария. Именно поэтому речь педагогов должна быть образной, богатой эмоционально и интон ...