Сведение матричной игры к задаче линейного программирования

Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом и, наоборот, каждая задача линейного программирования может быть представлена как конечная игра двух лиц с нулевой суммой. Рассмотрим игру двух лиц с нулевой суммой, заданную платежной матрицей

.

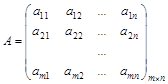Если платежная матрица не имеет седловой точки, т.е. a <b и , то решение игры представлено в смешанных стратегиях (x1, x2, ., xm) и (y1, y2, ., yn). Применение первым игроком оптимальной стратегии опт должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры.

, .

Рассмотрим задачу отыскания оптимальной стратегии игрока А, для которой имеют место ограничения

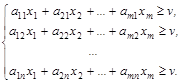
Величина v неизвестна, однако можно считать, что цена игры v > 0. Последнее условие выполняется всегда, если все элементы платежной матрицы неотрицательны, а этого можно достигнуть, прибавив ко всем элементам матрицы некоторое положительное число.

Преобразуем систему ограничений, разделив все члены неравенств на v.

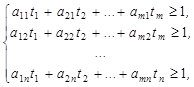(1)

где

, . (2)

По условию x1 + x2 + … +xm = 1.

Разделим обе части этого равенства на v.

.

Оптимальная стратегия (x1, x2, ., xm) игрока А должна максимизировать величину v, следовательно, функция

(3)

должна принимать минимальное значение.

Таким образом, получена задача линейного программирования: найти минимум целевой функции (3) при ограничениях (1), причем на переменные наложено условие неотрицательности (2). Решая ее, находим значения , и величину 1/v, затем отыскиваются значения xi = vti.

Аналогично для второго игрока оптимальная стратегия опт должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры.

, .

Рассмотрим задачу отыскания оптимальной стратегии игрока B, для которой имеют место ограничения

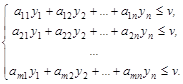
Преобразуем систему ограничений, разделив все члены неравенств на v.

Похожие статьи:

Методика проведения зачетного урока
Для систематического контроля за достижением обязательных результатов обучения в ходе учебного процесса целесообразно выбрать такую форму проверки, как зачет. Зачет – это специальный этап контроля, целью которого является проверка достижения учащимися уровня обязательной подготовки . С помощью заче ...

Особенности формирования связной речи у старших дошкольников с общим недоразвитием речи
Различные неблагоприятные воздействия, как во внутриутробном периоде развития, так и во время родов (родовая травма, асфиксия), а также в первые годы жизни ребенка могут приводить к общему недоразвитию. Общее недоразвитие речи – сложное речевое расстройство, при котором у детей с нормальным слухом ...

Сущность эстетических ценностей и идеалов человека
Категория «эстетические ценности» достаточно широко используется в современном научном лексиконе, однако это вовсе не значит, что она столь же стара, как мир. Обратимся к предыстории этого понятия. Эстетика как философская наука о прекрасном складывается в виде самостоятельной дисциплины лишь XVIII ...